In the realm of science and engineering, literal equations and dimensional analysis stand as indispensable tools for unraveling complex relationships and ensuring the validity of physical calculations. Literal equations provide a framework for expressing mathematical relationships between variables, while dimensional analysis ensures that these relationships are consistent with the fundamental units of measurement.
This comprehensive guide will delve into the concepts and applications of literal equations and dimensional analysis, empowering readers to navigate these powerful techniques with confidence.
Literal Equations

Literal equations are mathematical equations that involve variables representing unknown quantities. The purpose of literal equations is to solve for the value of one variable in terms of the other variables in the equation.
Examples of literal equations include:
- A = lw (area of a rectangle)
- V = lwh (volume of a rectangular prism)
- C = 2πr (circumference of a circle)
Dimensional Analysis, Literal equations and dimensional analysis
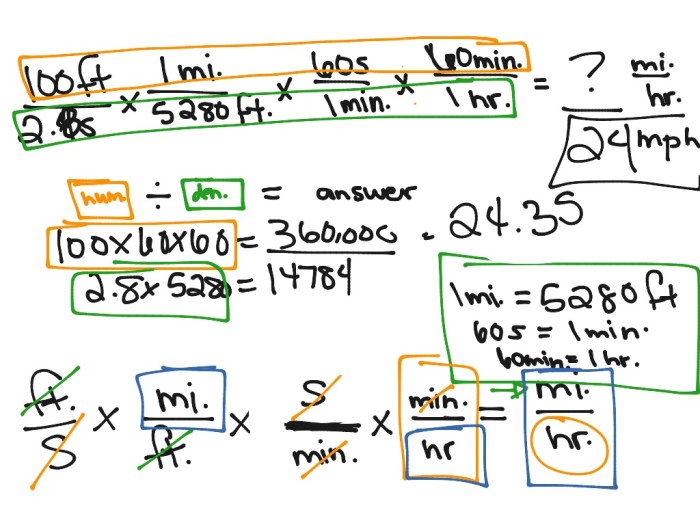
Dimensional analysis is a technique used to check the validity of equations and to convert units of measurement. The principles of dimensional analysis are based on the fact that the dimensions of the quantities on both sides of an equation must be the same.
Examples of dimensional analysis include:
- Checking the validity of the equation F = ma (force equals mass times acceleration)
- Converting units of measurement, such as converting miles per hour to kilometers per hour
Applications of Literal Equations and Dimensional Analysis
Literal equations are used in a wide variety of applications in science and engineering, including:
- Solving for unknown variables in equations
- Deriving relationships between variables
- Checking the validity of equations
- Converting units of measurement
Dimensional analysis is used in a wide variety of applications in science and engineering, including:
- Checking the validity of equations
- Converting units of measurement
- Deriving relationships between variables
- Solving for unknown variables in equations
Real-world examples of these applications include:
- Using literal equations to solve for the unknown side length of a rectangle
- Using dimensional analysis to check the validity of the equation F = ma
- Using dimensional analysis to convert units of measurement, such as converting miles per hour to kilometers per hour
Relationships between Literal Equations and Dimensional Analysis
Literal equations and dimensional analysis are closely related. Literal equations can be used to derive dimensional relationships, and dimensional analysis can be used to check the validity of literal equations.
For example, the literal equation A = lw can be used to derive the dimensional relationship that the area of a rectangle is proportional to the product of its length and width.
Dimensional analysis can also be used to check the validity of the literal equation F = ma. The dimensions of the quantities on the left-hand side of the equation (force) must be the same as the dimensions of the quantities on the right-hand side of the equation (mass times acceleration).
Advanced Concepts
Advanced concepts related to literal equations and dimensional analysis include:
- Dimensionless numbers
- Buckingham Pi theorem
- Similarity analysis
Dimensionless numbers are quantities that have no units. They are often used in fluid mechanics and heat transfer.
The Buckingham Pi theorem is a theorem that states that the number of independent dimensionless numbers that can be formed from a set of variables is equal to the number of variables minus the number of fundamental dimensions.
Similarity analysis is a technique that uses dimensional analysis to compare different systems that have the same governing equations.
Commonly Asked Questions: Literal Equations And Dimensional Analysis
What are literal equations used for?
Literal equations are used to express mathematical relationships between variables, independent of their numerical values.
How does dimensional analysis help ensure the validity of calculations?
Dimensional analysis ensures that the units of measurement in a calculation are consistent, preventing errors and ensuring the validity of the results.
Can literal equations be used to derive dimensional relationships?
Yes, literal equations can be used to derive dimensional relationships by equating the dimensions of both sides of the equation.