Three-dimensional figures and cross sections assignment – Embark on an enthralling journey into the realm of three-dimensional figures and cross sections, where geometry unveils its captivating secrets. This assignment invites you to delve into the intricacies of spatial forms and their enigmatic intersections, unlocking a world of real-world applications that will ignite your imagination and deepen your understanding of the physical world.
As we traverse this geometric landscape, we will define three-dimensional figures, unravel their defining characteristics, and encounter diverse examples that showcase their ubiquitous presence in our surroundings. We will then venture into the realm of cross sections, exploring their distinct types and the techniques employed to create them, empowering you with the tools to visualize and analyze three-dimensional objects from a new perspective.
Three-Dimensional Figures
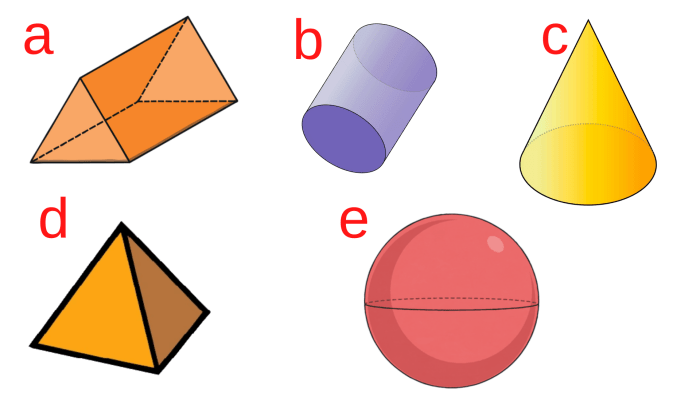
Three-dimensional figures, also known as solid figures, are geometric objects that have length, width, and height. They occupy space and have volume. Unlike two-dimensional figures, three-dimensional figures cannot be fully represented on a flat surface.
Characteristics of three-dimensional figures include:
- Length, width, and height
- Volume
- Faces, edges, and vertices
Examples of three-dimensional figures include cubes, spheres, cones, and pyramids.
Cross Sections
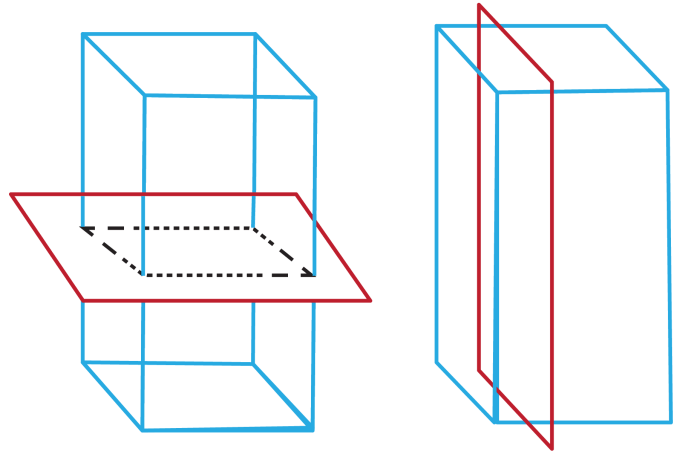
A cross section is a two-dimensional slice of a three-dimensional figure. It is created by cutting the figure along a plane. The shape of the cross section depends on the angle and position of the cut.
Different types of cross sections include:
- Axial cross section:A cross section that is parallel to the axis of symmetry of the figure.
- Equatorial cross section:A cross section that is perpendicular to the axis of symmetry of the figure.
- Oblique cross section:A cross section that is not parallel or perpendicular to the axis of symmetry of the figure.
To create a cross section, follow these steps:
- Choose a plane to cut the figure.
- Draw the Artikel of the cross section on the plane.
- Label the cross section with its type.
Three-Dimensional Figures and Cross Sections in Real-World Applications

Three-dimensional figures and cross sections are used in a variety of real-world applications, including:
- Architecture:Three-dimensional figures are used to design buildings and other structures. Cross sections are used to show the interior layout of buildings.
- Engineering:Three-dimensional figures are used to design machines and other objects. Cross sections are used to show the internal workings of machines.
- Medicine:Three-dimensional figures are used to create models of organs and other body parts. Cross sections are used to diagnose and treat medical conditions.
Understanding three-dimensional figures and cross sections is important in a variety of fields, including architecture, engineering, and medicine.
Assignment
For this assignment, you will create a cross section of a three-dimensional figure. You can choose any three-dimensional figure you like, but it must be a regular figure (i.e., a figure with all sides and angles equal). You will also need to label the cross section with its type.
Your assignment should be submitted in the following format:
- A drawing of the three-dimensional figure
- A drawing of the cross section
- A label indicating the type of cross section
The assignment is due on [due date].
FAQ: Three-dimensional Figures And Cross Sections Assignment
What are the key characteristics of three-dimensional figures?
Three-dimensional figures possess three dimensions: length, width, and height, allowing them to occupy space and have volume.
How are cross sections used in real-world applications?
Cross sections are employed in architecture, engineering, and medicine, among other fields, to visualize the internal structure of objects, plan constructions, and diagnose medical conditions.